MATeMAtyka 3. Zakres rozszerzony. Po gimnazjum
Matematyka / Podręcznik / Nowa Era
4
Jeśli kąt rozwarcia stożka ma 60°, to przekrój osiowy stożka jest trójkątem równobocznym
(wynika to stąd, że przekrój osiowy stożka to trójkąt równoramienny, którego kąt między ramionami to właśnie kąt rozwarcia stożka).
Tworząca stożka oraz średnica podstawy stożka mają więc jednakową długość:
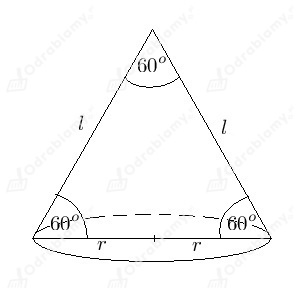
Zachodzi więc równość:
Wiemy, ile jest równe pole powierzchni bocznej, więc możemy zapisać równanie:
Wysokość ostrosłupa to wysokość trójkąta równobocznego o boku 4 cm.
Obliczamy objętość stożka:
5
Z treści zadania wiemy, że:
6
Tworząca stożka ma 50 cm. Średnica podstawy stożka ma 60 cm.
Promień podstawy stożka jest 2 razy krótszy od średnicy.
7
8
a)
Rysunek pomocniczy:
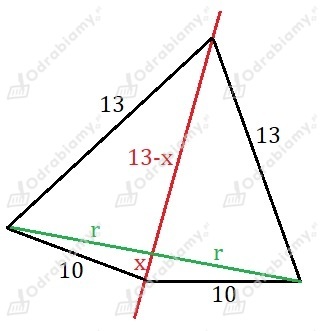
Korzystając z tw. Pitagorasa otrzymujemy:
9
Rysunek pomocniczy:

Z funkcji trygonometrycznych otrzymujemy:
10
Rysunek pomocniczy: