MATeMAtyka 3. Zakres rozszerzony. Po gimnazjum

Oznaczmy długość promienia podstawy jako r. Wiemy, ile wynosi pole podstawy, więc możemy zapisać:

     

 

Przekrój osiowy stożka to trójkąt równoramienny, którego podstawa jest średnicą podstawy stożka a ramiona są tworzącymi stożka. 

Jeśli trójkąt jest równoboczny, to średnica podstawy stożka i jego tworząca mają jednakową długość. 

Oznaczmy długość promienia podstawy walca jako r. 

 

 

Długość wysokości stożka oznaczmy jako h. 

 

 

   

Wiemy, że sinus kąta w trójkącie prostokątnym to stosunek długości przyprostokątnej naprzeciw kąta do długości przeciwprostokątnej. Mamy więc:

    

 

Obliczamy pole wycinka będącego powierzchnią boczną stożka:

    

Promień wycinka będącego powierzchnią boczną to zarazem tworząca stożka. 

 

 

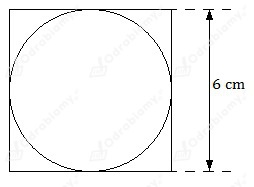
Największe koło, jakie można wyciąć z kwadratu o boku 6 cm, to koło o średnicy 6 cm. 

    

 

Przekrój osiowy stożka to trójkąt równoramienny, którego podstawa jest średnicą podstawy stożka, a ramiona to tworzące stożka. 

Jeśli trójkąt jest prostokątny równoramienny, to kąt rozwarcia stożka ma 90°, a kąty przy podstawie mają: