MATeMAtyka 3. Zakres rozszerzony. Po gimnazjum
Matematyka / Podręcznik / Nowa Era
2
Podstawą ostrosłupa prawidłowego czworokątnego jest kwadrat.
Oznaczmy długość krawędzi kwadratu jako a.
Z rysunku wnioskujemy, że ściany boczne ostrosłupa są trójkątami równobocznymi - także o boku a.
Wiemy, ile wynosi pole powierzchni całkowitej tego ostrosłupa, więc możemy zapisać równanie:
3
Wykonajmy rysunek pomocniczy - narysujmy ścianę boczną tego ostrosłupa.
Wysokość ściany bocznej oznaczyliśmy jako y.
Krawędź podstawy (a zarazem podstawę ściany bocznej) oznaczyliśmy jako 2x.
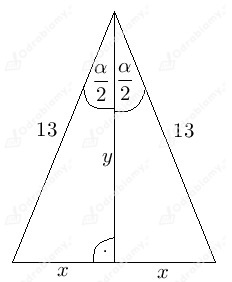
Wiemy, że:
Cosinus kąta w trójkącie prostokątnym to stosunek długości przyprostokątnej znajdującej się przy tym kącie do długości przeciwprostokątnej.
4
Rysunek pomocniczy:
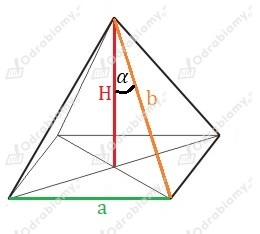
Zauważmy, że pole podstawy wynosi P, czyli:
5
Czworościan foremny to ostrosłup, którego wszystkie ściany są jednakowymi trójkątami równobocznymi.
Wykonajmy rysunek pomocniczy.
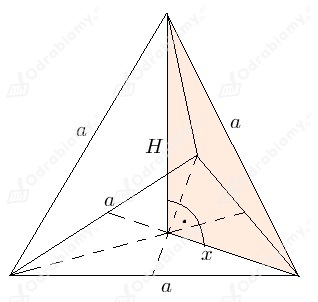
Odcinek x stanowi dwie trzecie wysokości trójkąta równobocznego o boku a.
6
Rysunek pomocniczy:
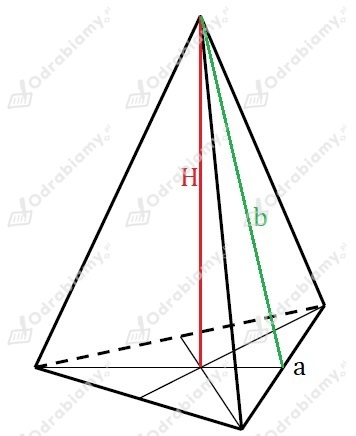
Z treści zadania wiemy, że:
7
Rysunek pomocniczy:
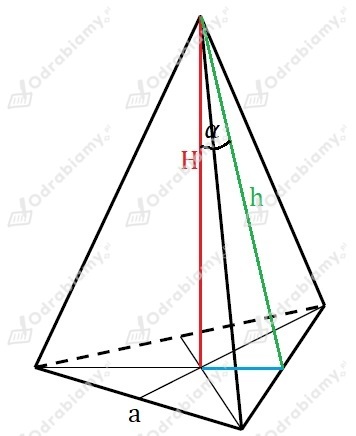
Zauważmy, że niebieski odcinek to
8
Rysunek pomocniczy:
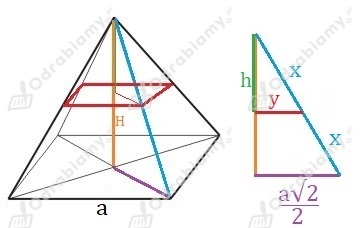
Z podobieństwa trójkątów otrzymujemy:
9