MATeMAtyka 3. Zakres rozszerzony. Po gimnazjum
Matematyka / Podręcznik / Nowa Era
6
Podstawą ostrosłupa prawidłowego pięciokątnego jest pięciokąt foremny.
Wiemy, że obwód tego pięciokąta jest równy 40 cm. Obliczmy, jaką długość ma bok tego pięciokąta:
7
Podstawą ostrosłupa prawidłowego sześciokątnego jest sześciokąt foremny.
Każdy sześciokąt foremny o boku a można podzielić na 6 jednakowych trójkątów równobocznych o boku a.
Promień koła opisanego na okręgu jest równy długości boku takiego trójkąta, ma więc długość a:
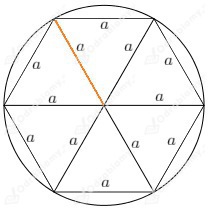
Promień koła wpisanego w sześciokąt foremny to wysokość jednego trójkąta:
8
Wiemy, że podstawą ostrosłupa jest wielokąt foremny. Nie wiemy, ile boków ma wielokąt foremny. Oznaczmy więc liczbę boków wielokąta foremnego jako k.
Zakładamy, że k jest równe co najmniej 3, ponieważ wielokąt ma najmniej trzy boki.
Wiemy, że obwód podstawy, czyli obwód wielokąta foremnego o k bokach, jest równy L.
9
Rysunek pomocniczy:
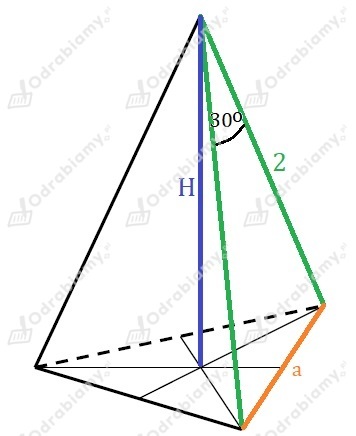
Obliczmy długość a, korzystając z twierdzenia cosinusów:
10
Zatem możemy obliczyć długość krawędzi podstawy.
Rysunek pomocniczy:
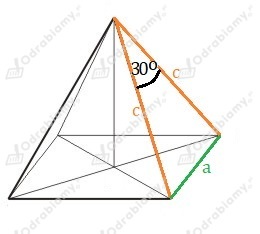
Korzystając z twierdzenia cosinusów, obliczmy długość krawędzi bocznej:
11
Rysunek pomocniczy:
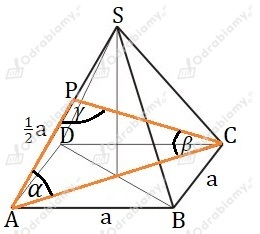
Obliczmy korzystając z twierdzenia cosinusów dla trójkąta ACS:
12
Obliczmy długość krawędzi AS korzystając z tw. Pitagorasa dla trójkąta ACS.
13