MATeMAtyka 3. Zakres rozszerzony. Po gimnazjum

Obliczmy pole podstawy ostrosłupa, czyli pole trójkąta równobocznego o boku 4 cm. 

 

 

Wiemy, że krawędź podstawy ostrosłupa ma 4 cm. Każda ze ścian bocznych ostrosłupa prawidłowego trójkątnego jest trójkątem równoramiennym.

Dodatkowo wiemy, że ściany boczne są trójkątami prostokątnymi. Kąt płaski przy wierzchołku ma więc miarę 90°.  

Podstawą ostrosłupa prawidłowego trójkątnego jest trójkąt równoboczny.

Oznaczmy długość boku tego trójkąta (czyli długość krawędzi ostrosłupa) jako a.

Korzystając ze wzoru na pole trójkąta równobocznego możemy zapisać równanie:

    

 

Czworościan foremny o krawędzi podstawy 5 cm ma cztery ściany w kształcie trójkąta równobocznego o boku 5 cm. 

Z rysunku możemy odczytać, że podstawą ostrosłupa jest prostokąt o wymiarach 8 x 5.

Ostrosłup jest prosty, więc wszystkie krawędzie boczne mają jednakową długość. Z rysunku odczytujemy, że krawędź boczna ma długość 5. 

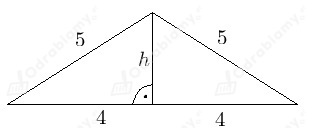
Mamy więc 2 ściany boczne będące trójkątami równobocznymi o boku 5 oraz 2 ściany boczne będące trójkątami równoramiennymi o podstawie 8 i ramieniu 5. 

Korzystając z twierdzenia Pitagorasa obliczmy wysokość drugiego z tych trójkątów:

Obliczmy, jaką długopść ma przekątna podstawy, czyli przekątna prostokąta o bokach 6 cm i 8 cm. 

Wystarczy skorzystać z twierdzenia Pitagorasa. 

 

Ostrosłup prosty, to ostrosłup, którego wszystkie krawędzie boczne mają taką samą długość.

Należy pokazać, że wszystkie wierzchołki podstawy leżą w takiej samej odległości od spodka wysokości.

Dla ostrosłupa trójkątnego otrzymujemy:

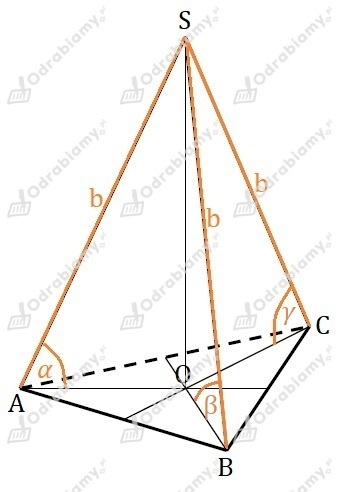
Zauważmy, że

 

 

 

Wykonajmy rysunek pomocniczy:

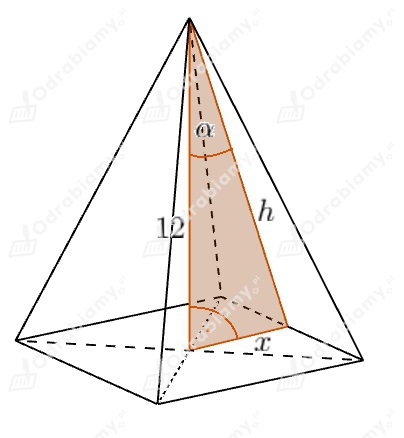
Wiemy, że:

    

Sinus kąta w trójkącie prostokątnym to stosunek długości przeciwprostokątnej naprzeciwko tego kąta do długości przeciwprostokątnej:

     

Wykonajmy rysunek pomocniczy:

  

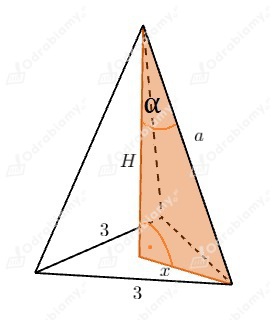
Odcinek x stanowi dwie trzecie wysokości podstawy, czyli dwie trzecie wysokości trójkąta równobocznego o boku 3:

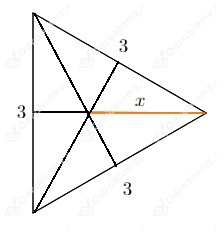
Korzystając ze wzoru na wysokość trójkąta równobocznego obliczmy, jaką długość ma odcinek x: