MATeMAtyka 3. Zakres rozszerzony. Po gimnazjum
Matematyka / Podręcznik / Nowa Era
Ćwiczenie 5
Podstawą graniastosłupa prawidłowego sześciokątnego jest sześciokąt foremny.
Każdy sześciokąt foremny o boku a można podzielić na 6 jednakowych trójkątów równobocznych o boku a:
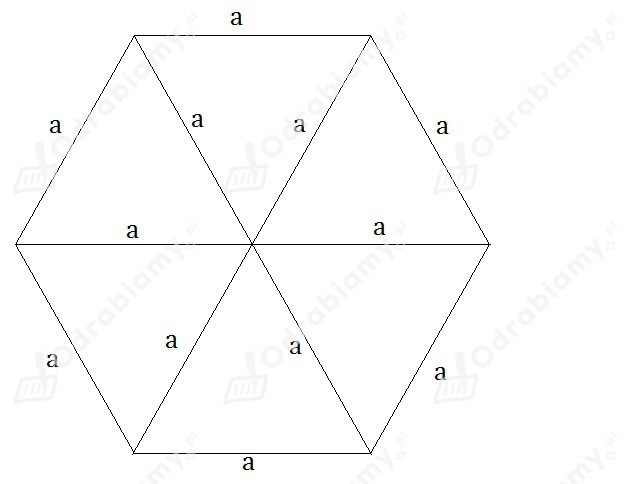
Pole sześciokąta foremnego o boku a jest więc dane wzorem:
1
a)
Korzystając z twierdzenia Pitagorasa obliczymy, jaką długość ma wysokość trapezu:
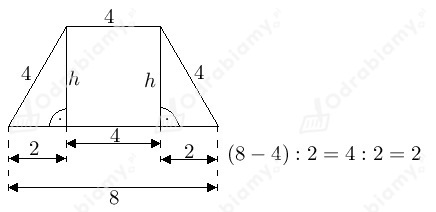
2
Wysokość graniastosłupa ma 12 cm, a przekątna ściany bocznej ma 15 cm.
Ściana boczna jest więc prostokątem o jednym boku 12 cm i przekątnej 15 cm.
Obliczmy długość drugiego boku - będzie to zarazem długość krawędzi podstawy graniastosłupa.
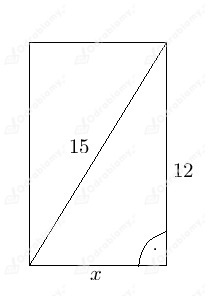
3
Podstawą graniastosłupa prawidłowego czworokątnego jest kwadrat.
Jeśli pole tego kwadratu wynosi 16 cm², to bok tego kwadratu ma 4 cm.
Oznaczmy długość krawędzi bocznej (czyli wysokości tego graniastosłupa) jako h.
Korzystając ze wzoru na długość przekątnej prostopadłościanu możemy zapisać:
4
Rysunek pomocniczy podstawy tego graniastosłupa:
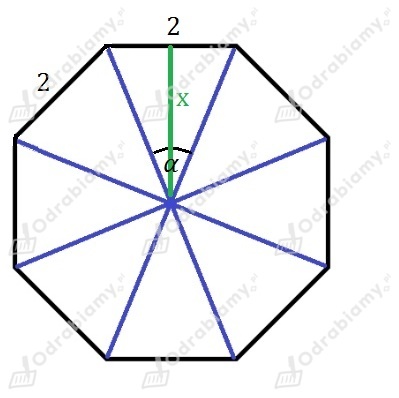
Obliczmy miarę kąta :
Wobec tego z funkcji trygonometrycznych otrzymujemy: