MATeMAtyka 3. Zakres rozszerzony. Po gimnazjum
Matematyka / Podręcznik / Nowa Era
1
Podstawą graniastosłupa prawidłowego czworokątnego jest kwadrat.
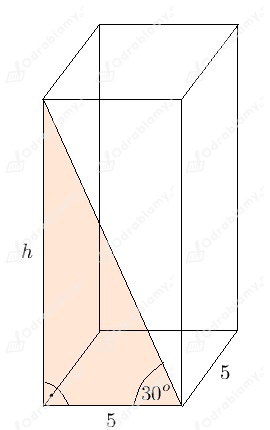
Możemy obliczyć, jaką długość ma wysokość, korzystając z funkcji trygonometrycznych:
2
Jeśli graniastosłup jest prawidłowy czworokątny, to jego podstawą jest kwadrat.
Oznaczmy długość krawędzi podstawy jako x.
Wysokość graniastosłupa oznaczmy jako h.
Chcemy pokazać, że graniastosłup jest sześcianem, czyli, że x=h (ma wszystkie krawędzie jednakowej długości).
Zapiszmy oznaczenia na rysunku:
3
Graniastosłup prawidłowy czworokątny to graniastosłup, którego podstawą jest kwadrat. Bok kwadratu ma długość 4 cm.
Wiemy, że przekątna kwadratu o boku a ma długość a√2. Przekątna kwadratu o boku 4 ma więc długość 4√2 cm.
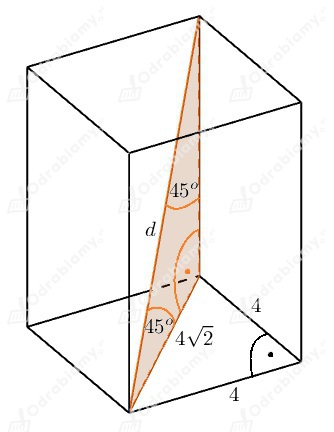
Zamalowany na pomarańczowo trójkąt jest prostokątny równoramienny.
Przeciwprostokątna w trójkącie prostokątnym równoramiennym o przyprostokątnej b ma długość b√2.
4
Podstawą graniastosłupa prawidłowego sześciokątnego jest sześciokąt foremny.
Najpierw zajmiemy się przekątną BE1.
Zauważmy, że trójkąt E₁BB₁ jest prostokątny. Odcinek E₁B₁ to dłuższa przekątna sześciokąta foremnego o boku 4 cm. Każdy sześciokąt foremny można podzielić na 4 jednakowe trójkąty równoboczne. Odcinek E₁B₁ składa się wtedy z dwóch boków trójkąta równobocznego, ma więc długość 8 cm.
5
Korzystając z twierdzenia Pitagorasa obliczymy, jaką długość ma dłuższa przekątna podstawy graniastosłupa.
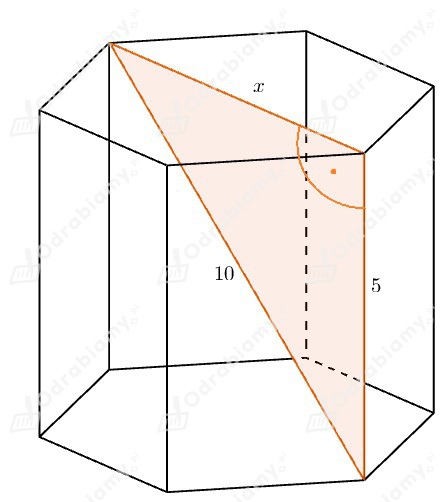
6
Graniastosłup prawidłowy czworokątny to graniastosłup, którego podstawa jest kwadratem.
Oznaczmy długość krawędzi podstawy tego graniastosłupa (wyrażoną w cm) jako x, a wysokość (wyrażoną w cm) jako h.
Wtedy pole podstawy graniastosłupa jest równe:
Na pole boczne składają się pola czterech prostokątów o bokach h i x.
Na pole powierzchni całkowitej składają się 2 pola podstawy i pole powierzchni bocznej.
7
Rysunek pomocniczy:
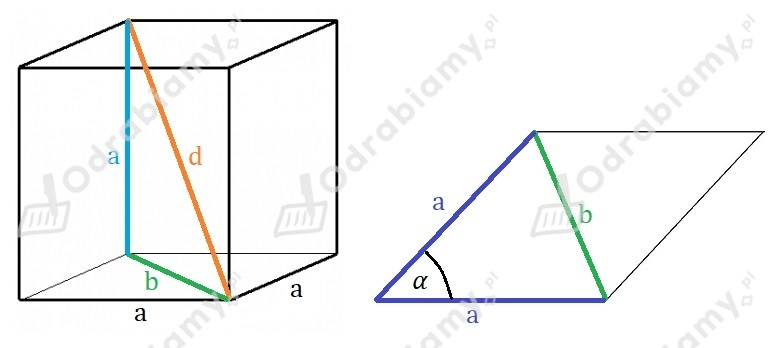
Obliczmy długość b, korzystając z twierdzenia cosinusów.
8
Rysunek pomocniczy:
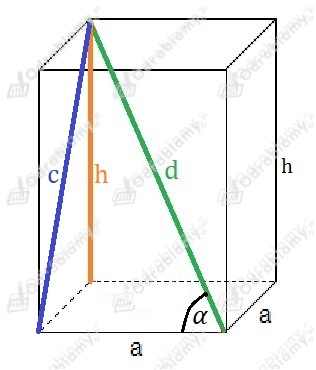
Z twierdzenia Pitagorasa otrzymujemy:
oraz