MATeMAtyka 3. Zakres rozszerzony. Po gimnazjum

Podstawa graniastosłupa to trójkąt równoramienny o ramionach 8 cm i kącie 120°. 

Obliczmy, jaka jest miara kąta przy podstawie w tym trójkącie

(korzystamy z tego, że suma miar wszystkich kątów w trójkącie jest równa 180°,

a kąty przy podstawie w trójkącie równoramiennym mają jednakowe miary). 

   

Wiemy, że podstawą graniastosłupa jest romb o kącie ostrym 30° i boku 12 cm. Wykonajmy rysunek pomocniczy:

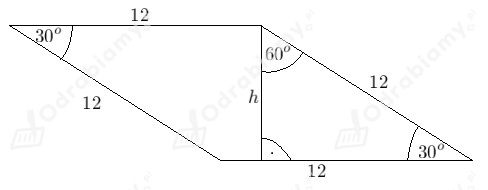
Korzystając z zależności między długościami boków w trójkącie o kątach 90°, 60° 30° możemy obliczyć, 

 

Oznaczmy długość wysokości tego graniastosłupa (wyrażoną w cm) jako H. 

Wtedy możemy zapisać równanie:

 

 

Podstawą graniastosłupa jest trójkąt równoboczny o boku 6. Wysokość graniastosłupa ma długość 10.

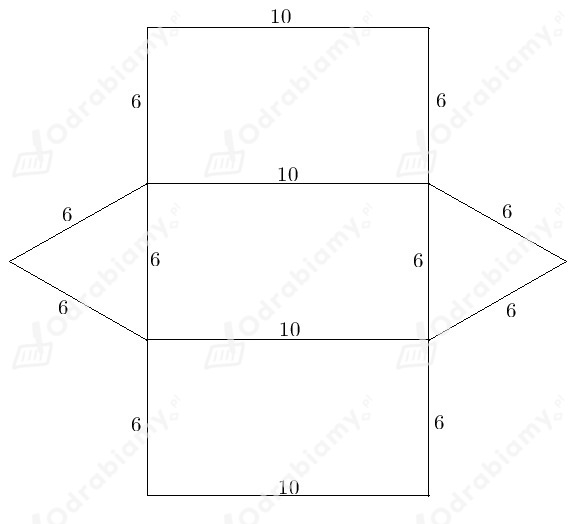
Obliczmy pole podstawy, korzystając ze wzoru na pole trójkąta równobocznego:

      

 

Podstawą graniastosłupa prawidłowego sześciokątnego jest sześciokąt foremny. 

Aby narysować sześciokąt foremny, wystarczy skorzystać z tego, że każdy sześciokąt foremny można podzielić na 6 jednakowych trójkątów równobocznych.

Poniżej zamieszczamy opis, jak narysować sześciokąt foremny o boku 3 cm.